Solid harmonics
In physics and mathematics, the solid harmonics are solutions of the Laplace equation in spherical polar coordinates. There are two kinds: the regular solid harmonics 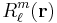 , which vanish at the origin and the irregular solid harmonics
, which vanish at the origin and the irregular solid harmonics 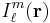 , which are singular at the origin. Both sets of functions play an important role in potential theory, and are obtained by rescaling spherical harmonics appropriately:
, which are singular at the origin. Both sets of functions play an important role in potential theory, and are obtained by rescaling spherical harmonics appropriately:
Contents |
Derivation, relation to spherical harmonics
Introducing r, θ, and φ for the spherical polar coordinates of the 3-vector r, we can write the Laplace equation in the following form
where L2 is the square of the angular momentum operator,
It is known that spherical harmonics Yml are eigenfunctions of L2,,
Substitution of Φ(r) = F(r) Yml into the Laplace equation gives, after dividing out the spherical harmonic function, the following radial equation and its general solution,
The particular solutions of the total Laplace equation are regular solid harmonics:
and irregular solid harmonics:
Racah's normalization (also known as Schmidt's semi-normalization) is applied to both functions
(and analogously for the irregular solid harmonic) instead of normalization to unity. This is convenient because in many applications the Racah normalization factor appears unchanged throughout the derivations.
Addition theorems
The translation of the regular solid harmonic gives a finite expansion,
where the Clebsch-Gordan coefficient is given by
The similar expansion for irregular solid harmonics gives an infinite series,
with 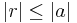 . The quantity between pointed brackets is again a Clebsch-Gordan coefficient,
. The quantity between pointed brackets is again a Clebsch-Gordan coefficient,
References
The addition theorems were proved in different manners by many different workers. See for two different proofs for example:
- R. J. A. Tough and A. J. Stone, J. Phys. A: Math. Gen. Vol. 10, p. 1261 (1977)
- M. J. Caola, J. Phys. A: Math. Gen. Vol. 11, p. L23 (1978)
Real form
By a simple linear combination of solid harmonics of ±m these functions are transformed into real functions. The real regular solid harmonics, expressed in cartesian coordinates, are homogeneous polynomials of order l in x, y, z. The explicit form of these polynomials is of some importance. They appear, for example, in the form of spherical atomic orbitals and real multipole moments. The explicit cartesian expression of the real regular harmonics will now be derived.
Linear combination
We write in agreement with the earlier definition
with
where 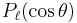 is a Legendre polynomial of order l. The m dependent phase is known as the Condon-Shortley phase.
is a Legendre polynomial of order l. The m dependent phase is known as the Condon-Shortley phase.
The following expression defines the real regular solid harmonics:
and for m = 0:
Since the transformation is by a unitary matrix the normalization of the real and the complex solid harmonics is the same.
z-dependent part
Upon writing u = cos θ the mth derivative of the Legendre polynomial can be written as the following expansion in u
with
Since z = r cosθ it follows that this derivative, times an appropriate power of r, is a simple polynomial in z,
(x,y)-dependent part
Consider next, recalling that x = r sinθcosφ and y = r sinθsinφ,
Likewise
Further
and
In total
List of lowest functions
We list explicitly the lowest functions up to and including l = 5 . Here ![\bar{\Pi}^m_\ell(z) \equiv \left[\tfrac{(2-\delta_{m0}) (\ell-m)!}{(\ell%2Bm)!}\right]^{1/2} \Pi^m_{\ell}(z) .](/2012-wikipedia_en_all_nopic_01_2012/I/f0689759a40da2ffbed04aa8843d7255.png)
The lowest functions 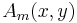 and
and 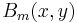 are:
are:
-
-
-
-
m Am Bm 0 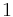
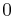
1 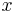
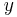
2 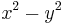
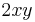
3 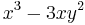
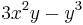
4 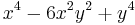
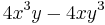
5 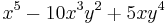
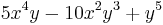
-
-
-
Examples
Thus, for example, the angular part of one of the nine normalized spherical g atomic orbitals is:
One of the 7 components of a real multipole of order 3 (octupole) of a system of N charges qi is
Spherical harmonics in Cartesian form
The following expresses normalized spherical harmonics in Cartesian coordinates (Condon-Shortley phase):
and for m = 0:
Here
and for m > 0:
For m = 0:
Examples
Using the expressions for 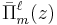 ,
, 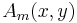 , and
, and 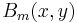 listed explicitly above we obtain:
listed explicitly above we obtain:
It may be verified that this agrees with the function listed here and here.
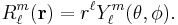
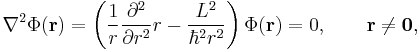
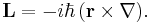
![L^2 Y^m_{\ell}\equiv \left[ L^2_x %2BL^2_y%2BL^2_z\right]Y^m_{\ell} = \ell(\ell%2B1) Y^m_{\ell}.](/2012-wikipedia_en_all_nopic_01_2012/I/9d1436ba555cd04857277c3371c013c1.png)
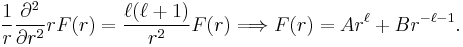
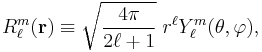
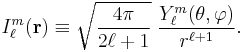
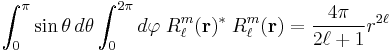
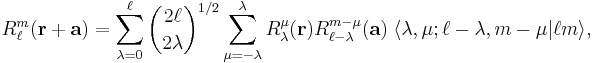
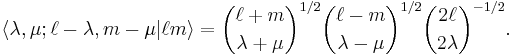
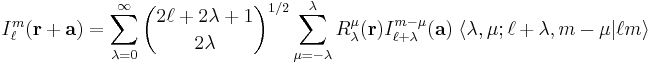
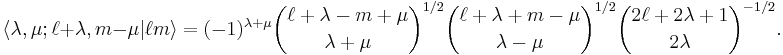
![\Theta_{\ell}^m (\cos\theta) \equiv \left[\frac{(\ell-m)!}{(\ell%2Bm)!}\right]^{1/2} \,\sin^m\theta\, \frac{d^m P_\ell(\cos\theta)}{d\cos^m\theta}, \qquad m\ge 0,](/2012-wikipedia_en_all_nopic_01_2012/I/02a77c91241732ba10a075902a0aec1c.png)
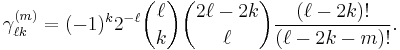
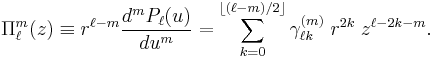
![r^m \sin^m\theta \cos m\varphi = \frac{1}{2} \left[ (r \sin\theta e^{i\varphi})^m
%2B (r \sin\theta e^{-i\varphi})^m \right] =
\frac{1}{2} \left[ (x%2Biy)^m %2B (x-iy)^m \right]](/2012-wikipedia_en_all_nopic_01_2012/I/dfd1aea0e6f95b199e39761c6c8f0968.png)
![r^m \sin^m\theta \sin m\varphi = \frac{1}{2i} \left[ (r \sin\theta e^{i\varphi})^m
- (r \sin\theta e^{-i\varphi})^m \right] =
\frac{1}{2i} \left[ (x%2Biy)^m - (x-iy)^m \right].](/2012-wikipedia_en_all_nopic_01_2012/I/85d42914755b1347970e19483b6d5915.png)
![A_m(x,y) \equiv
\frac{1}{2} \left[ (x%2Biy)^m %2B (x-iy)^m \right]= \sum_{p=0}^m \binom{m}{p} x^p y^{m-p} \cos (m-p) \frac{\pi}{2}](/2012-wikipedia_en_all_nopic_01_2012/I/3a25f7e174add17be597ee857ba82d65.png)
![B_m(x,y) \equiv
\frac{1}{2i} \left[ (x%2Biy)^m - (x-iy)^m \right]= \sum_{p=0}^m \binom{m}{p} x^p y^{m-p} \sin (m-p) \frac{\pi}{2}.](/2012-wikipedia_en_all_nopic_01_2012/I/396066928ca77a858c5f86eea8ab91d2.png)
![C^m_\ell(x,y,z) = \left[\frac{(2-\delta_{m0}) (\ell-m)!}{(\ell%2Bm)!}\right]^{1/2} \Pi^m_{\ell}(z)\;A_m(x,y),\qquad m=0,1, \ldots,\ell](/2012-wikipedia_en_all_nopic_01_2012/I/428a7f7aff8aec77ae8b00ff442526fc.png)
![S^m_\ell(x,y,z) = \left[\frac{2 (\ell-m)!}{(\ell%2Bm)!}\right]^{1/2} \Pi^m_{\ell}(z)\;B_m(x,y)
,\qquad m=1,2,\ldots,\ell.](/2012-wikipedia_en_all_nopic_01_2012/I/db64065a519539ef5a9a3a26d49d0d0e.png)
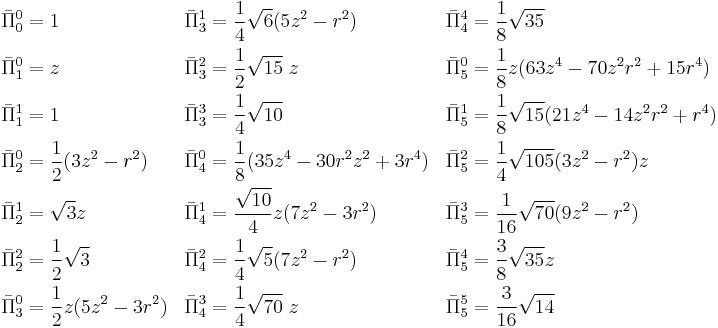
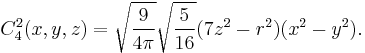
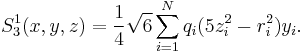
![r^\ell\,
\begin{pmatrix}
Y_\ell^{m} \\
Y_\ell^{-m}
\end{pmatrix}
=
\left[\frac{2\ell%2B1}{4\pi}\right]^{1/2} \bar{\Pi}^m_\ell(z)
\begin{pmatrix}
(-1)^m (A_m %2B i B_m) \\
\qquad (A_m - i B_m) \\
\end{pmatrix} ,
\qquad m > 0.](/2012-wikipedia_en_all_nopic_01_2012/I/70278b8a5be7eac84cc81ebe5317b5ee.png)
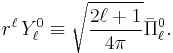
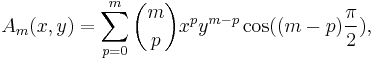
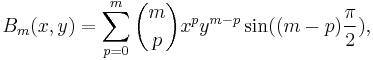
![\bar{\Pi}^m_\ell(z)
= \left[\frac{(\ell-m)!}{(\ell%2Bm)!}\right]^{1/2}
\sum_{k=0}^{\left \lfloor (\ell-m)/2\right \rfloor}
(-1)^k 2^{-\ell} \binom{\ell}{k}\binom{2\ell-2k}{\ell} \frac{(\ell-2k)!}{(\ell-2k-m)!}
\; r^{2k}\; z^{\ell-2k-m}.](/2012-wikipedia_en_all_nopic_01_2012/I/0232bce1152949a4eaea8a98e976c57d.png)
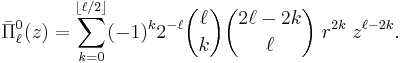
![Y^1_3 = - \frac{1}{r^3} \left[\tfrac{7}{4\pi}\cdot \tfrac{3}{16} \right]^{1/2} (5z^2-r^2)(x%2Biy) =
- \left[\tfrac{7}{4\pi}\cdot \tfrac{3}{16}\right]^{1/2} (5\cos^2\theta-1) (\sin\theta e^{i\varphi})](/2012-wikipedia_en_all_nopic_01_2012/I/01a36ea25d17997de3fc7af29efc835b.png)
![Y^{-2}_4 = \frac{1}{r^4} \left[\tfrac{9}{4\pi}\cdot\tfrac{5}{32}\right]^{1/2}(7z^2-r^2) (x-iy)^2
= \left[\tfrac{9}{4\pi}\cdot\tfrac{5}{32}\right]^{1/2}(7 \cos^2\theta -1) (\sin^2\theta e^{-2 i \varphi})](/2012-wikipedia_en_all_nopic_01_2012/I/26e0b6b3459eb5f9c21c445ca7e4749a.png)